![]()
Per scomporre questo dobbiamo utilizzare Ruffini. Analizziamo prima le possibili radici con il teorema del resto, con i valori ![]() .
.
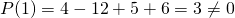 non accettabile
non accettabile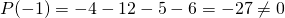 non accettabile
non accettabile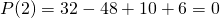 accettabile.
accettabile.
Ora usiamo Ruffini per abbassarlo di grado:
Quindi:
![]() .
.
Distinguiamo in due casi separati e otteniamo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
In conclusione:
![]()
avrà come soluzioni:
![]()
![]()
![]()
Altri esercizi simili:
- Equazioni abbassabili di grado 1
- Equazioni abbassabili di grado 2
- Equazioni abbassabili di grado 3
- Equazioni abbassabili di grado 4
- Equazioni abbassabili di grado 5
- Equazioni abbassabili di grado 6
- Equazioni abbassabili di grado 7
- Equazioni abbassabili di grado 8
- Equazioni abbassabili di grado 9
- Equazioni abbassabili di grado 10
(Questa pagina è stata visualizzata da 178 persone)