Equazione biquadratica 10

$9x^2+1=(3-x^2)(x^2+4)$

$9x^2+1=3x^2+12-x^4-4x^2$

$x^4+9x^2-3x^2+4x^2+1-12=0$

$x^4+10x^2-11=0$

Risolviamola come equazione di secondo grado:

$a=1$

$b=10$

$c=-11$

$x^2_{\frac 12}=\frac {-10 \pm \sqrt {100+44}}{2}$

$x^2_{\frac 12}=\frac {-10 \pm \sqrt {144}}{2}$

$x^2_{\frac 12}=\frac {-10 \pm 12}{2}$

$x^2_1=\frac {-10 - 12}{2}=\frac {-22}2=-11$

$x^2_2=\frac {-10 + 12}{2}=\frac 22=1$

Quindi, possiamo riscrivere

$x^4+10x^2-11=(x^2+11)(x^2-1)$

Distinguendo i due casi otteniamo:

Equazione impossibile in quanto il 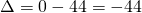$\Delta=0-44=-44$ è negativo.

$x^2=1$

$x=\pm 1$

Altri esercizi simili:

(Questa pagina è stata visualizzata da 241 persone)

Matebook