Definiamo semplicemente un’equazione letterale quando, oltre a numeri ed incognite, compaiono anche altre lettere.
E’ necessario tenere presente che la lettera rappresenta in tutto e per tutto un numero, e che, quindi, nel caso di applicazione del secondo principio di equivalenza, non sempre si possa dividere per un determinato valore della lettera (ovvero si dovranno escludere quei valori delle lettere che rendono nullo il denominatore!!!).
Quindi, nella risoluzione di un’equazione i procedimenti non variano di una virgola; cambia solo la discussione finale per le quali bisogna capire per quali valori della lettera l’equazione diventa possibile, impossibile e/o indeterminata.
![]() .
.
Per ![]() , l’equazione diventerebbe
, l’equazione diventerebbe ![]() , quindi, unendo i risultati otteniamo:
, quindi, unendo i risultati otteniamo:
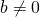 equazione determinata e
equazione determinata e 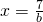
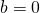 equazione impossibile.
equazione impossibile.
![]() . Quindi:
. Quindi:
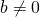 equazione determinata e
equazione determinata e 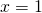
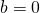 equazione indeterminata.
equazione indeterminata.
![]() . Quindi:
. Quindi:
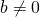 , equazione determinata e
, equazione determinata e 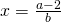 ;
;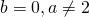 , equazione impossibile;
, equazione impossibile;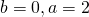 equazione indeterminata.
equazione indeterminata.
![]() . Quindi:
. Quindi:
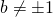 , equazione determinata e
, equazione determinata e 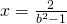
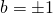 , equazione impossibile.
, equazione impossibile.
![]() . Quindi:
. Quindi:
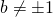 , equazione determinata e
, equazione determinata e 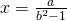
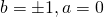 , equazione indeterminata;
, equazione indeterminata;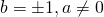 , equazione impossibile.
, equazione impossibile.
![]() . Quindi:
. Quindi:
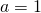 equazione indeterminata;
equazione indeterminata;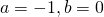 equazione indeterminata;
equazione indeterminata;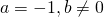 equazione impossibile;
equazione impossibile;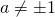 , equazione determinata, e
, equazione determinata, e 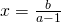
- Sistemi di grado superiore al secondo
- Monomi
- Polinomi
- Equazioni di primo grado
- Equazioni di primo grado fratte
- Equazioni di primo grado letterali
- Sistemi di equazioni di primo grado
- Disequazioni
- Sistemi di disequazioni di primo grado
- Radicali
- Equazioni di secondo grado
- Disequazioni di secondo grado
- Equazioni di primo grado trigonometriche
- Sistemi di secondo grado
- Equazioni di grado superiore al secondo
- Disequazioni goniometriche
(Questa pagina è stata visualizzata da 523 persone)