Equazioni di secondo grado

-2

Si definisce equazione di secondo grado un’uguaglianza in una sola incognita x della forma

ax^2+bx+c=0, a\neq 0.

Un’equazione di secondo grado avrà al massimo due soluzioni dette radici, a seconda del segno del discriminante pari a:

\Delta = b^2 - 4ac.

Le radici si calcolano con la seguente formula:

x_{\frac 12}=\frac{-b\pm\sqrt{\Delta}}{2a}.

Dalla precedente risulta evidente che se dovesse essere \Delta=0

x_{1}=\frac{-b+\sqrt{0}}{2a}\Rightarrow x_{1}=\frac{-b}{2a}

 

x_{2}=\frac{-b-\sqrt{0}}{2a}\Rightarrow x_{2}=\frac{-b}{2a}

 

e quindi x_{1}=x_{2}.

  • L’equazione avrà due soluzioni reali e distinte solo se \Delta>0.
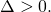
  • L’equazione avrà due soluzioni reali e coincidenti solo se \Delta =0.
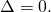
  • L’equazione non avrà nessuna soluzione reale solo se \Delta <0.
Elenchiamo adesso 3 casi particolari di equazioni di secondo grado incomplete:
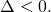
  • Si dice spuria un’equazione avente 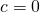c=0; si presenta quindi nella forma

ax^2+bx=0.

In questo caso si procede mettendo  a fattor comune totale x:

x(ax+b)=0

per la legge di annulamento del prodotto si ha

x=0 \wedge ax+b=0

Le soluzioni sono quindi x=0 \wedge x=-\frac{b}{a}.

  • Si dice pura un’equazione avente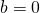b=0, si presenta quindi nella forma

ax^2+c=0.

Procedendo si ha:

ax^2=-c \Rightarrow x=\pm\sqrt{\frac{-c}{a}}.

Ovviamente il tutto avrà senso solo se \frac{-c}{a}>0 altrimenti la radice non è possibile calcolarla, e quindi l’equazione sarà impossibile.

 

  • Si dice monomia un’equazione avente 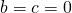b=c=0 e si presenta quindi nella forma:
ax^2=0
Procedendo si ottiene:
x_{\frac 12} = 0

 Formula ridotta

Infine, se notiamo che il coefficiente della x è pari, potremmo utilizzare per comodità la formula ridotta:

x_{\frac 12}= \frac {-\frac b2 \pm \sqrt {(\frac b2)^2-ac}}{a}

 

 

(Questa pagina è stata visualizzata da 782 persone)

Lascia un commento