Esercizi equazioni di secondo grado: Problema 5 di geometria piana

-5

Soluzione e svolgimento del seguente problemi di geometria piana.

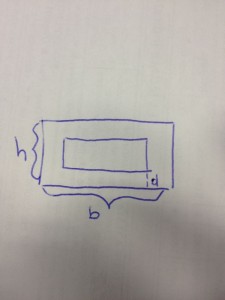
Un rettangolo ha il perimetro di 80 cm e la base di 26 cm. Determinare i lati di un secondo rettangolo interno al data, con i lati equidistanti dai lati del primo e di area 28 cm $^2$

Sia $2p$ il perimetro, $b$ la base e $h$ l’altezza del primo rettangolo.

Dai dati otteniamo che:

$2p=80 \mbox { cm}$

$b=26 \mbox { cm}$

e quindi:

$2p=2b+2h=80 \mbox { cm}$

$2h+52 \mbox { cm} = 80 \mbox { cm}$

$2h=(80-52)\mbox { cm}$

$2h=28 \mbox { cm}$

$h=14\mbox { cm}$

Ora, visto che il rettangolo è all’interno dell’altro, e ogni lato deve essere equidistante dai lati di quello esterno, possiamo chiamare la distanza con $2d$ (usiamo il 2 perchè le distanze ci sono da ambo le parti del rettangolo), così i lati $x$ e $y$ del nuovo rettangolo saranno:

$x=b-2d$

$y=h-2d$

Quindi il calcolo dell’area del rettangolo interno sarà (evito per comodità di usare le unità di misura…):

$A=x*y=(b-2d)(h-2d)=(14-2d)(26-2d)=4d^2-40(2d)+364=28$

$(2d)^2-40(2d)+336=0$

$2d_{\frac 1 2} =\frac {40\pm \sqrt {1600-1344}}{2}=\frac {40\pm \sqrt {256}}{2}=\frac {40\pm 16}{2}$

$2d_1=\frac {40+16}{2}=\frac {56}{2}=28$

$2d_2=\frac {40-16}{2}=\frac {24}{2}=12$

$2d_1$ è una soluzione non accettabile perchè, ricordando che questo valore rappresenta la distanza tra i due lati dei rettangoli, questo valore farebbe si che il lato del rettangolo interno abbia misura negativo.