Esercizi equazioni di secondo grado: Problema 7 di geometria piana

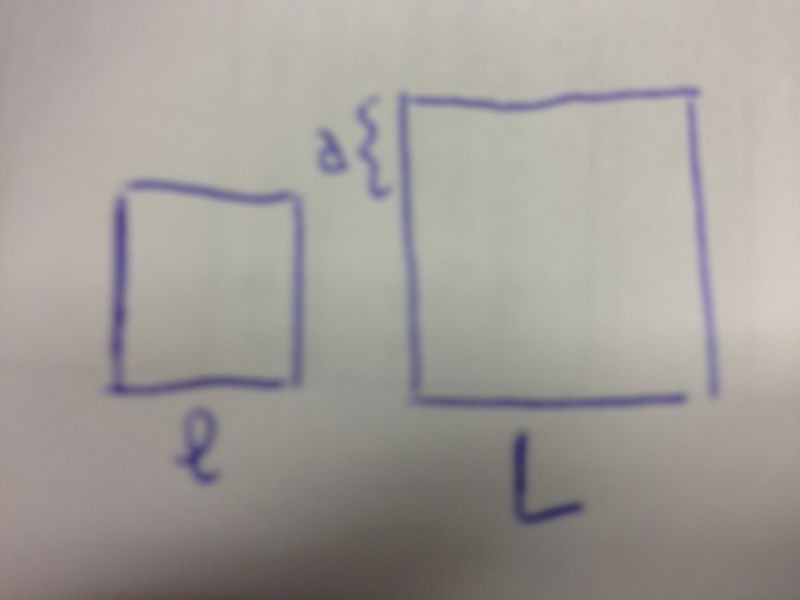
I lati di due quadrati differiscono di a, la somma delle loro aree è 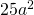$25a^2$ ; trovare i lati dei due quadrati

Definiamo con $l$ e $L$ i lati dei due quadrati dove $L$ rappresenta il lato del quadrato più grande. Dai dati otteniamo:

$L=l+a$

$l^2+L^2=25a^2$

Sostituiamo nella seconda equazione il valore di $L$ , ottenendo così l’equazione:

$l^2+(l+a)^2=25a^2$

$l^2+l^2+2al+a^2-25a^2=0$

$2l^2+2al-24a^2=0$

$l^2+al-12a^2=0$

$l_\frac 1 2 =\frac {-a \pm \sqrt {1+48 a^2}}{2}$

$l_\frac 1 2 =\frac {-a \pm \sqrt {49 a^2}}{2}$

$l_\frac 1 2 =\frac {-a \pm 7a}{2}$

$l_1= \frac {-a+7a}{2}=\frac {6a}{2}=3a$

$l_2=\frac {-a-7a}{2}=\frac {-8a}{2}=-4a$

Ovviamente la soluzione accettabile è solo $l_1$ in quanto un lato di un quadrato non può avere misura negativa.

Di conseguenza, i lati dei due quadrati saranno:

$l=3a$

$L=3a+a=4a$ .

Altri esercizi simili:

(Questa pagina è stata visualizzata da 818 persone)

Matebook