Esercizi equazioni di secondo grado: Problema 8 di geometria piana

Soluzione e svolgimento del seguente problemi di geometria piana.

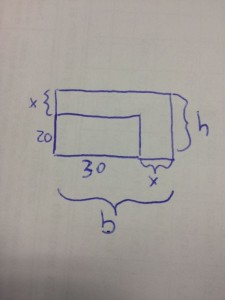
I lati di un rettangolo sono lunghi 20 cm e 30 cm. Aumentando i lati di due segmenti di eguale lunghezza, l’area aumenta di 336 cm $^2$ . Calcolare le lunghezze di tali segmenti.

Definendo con $b$ e $h$ la base e l’altezza del nuovo rettangolo, con $A_r$ l’area del primo rettangolo, con $A_R$ l’area del rettangolo allungato e con $x$ l’aumento della lunghezza dei lati otteniamo che (tralascio, ove possibile per evitare problemi di visualizzazione, le unità di misura):

$b=20 +x$

$h=30+x$

$A_R=A_r+336 \mbox { cm}^2$

$b*h=[(20*30)+336] \mbox { cm}^2=(600+336)\mbox { cm}^2=936\mbox { cm}^2$

Sostituendo nell’equazione dell’area le prime due, otteniamo:

$(20+x)(30+x)=936$

$600+20x+30x+x^2-936=0$

$x^2+50x-336=0$

$x_\frac 1 2 =\frac {-50\pm \sqrt {2500+1344}}{2}$

$x_\frac 1 2 =\frac {-50\pm \sqrt {3844}}{2}$

$x_\frac 1 2 =\frac {-50\pm 62}{2}$

$x_1=\frac {-50+62}{2}=\frac {12}{2}=6$

$x_2=\frac {-50-62}{2}=\frac {-112}{2}=-56$

Ovviamente $x_2$ non è accettabile come soluzione in quanto un aumento non può essere negativo.

Di conseguenza l’unica soluzione accettabile è: $x=6 \mbox { cm}$ , di conseguenza le due nuove dimensioni del rettangolo saranno:

$b=26 \mbox { cm}$

$h=36 \mbox { cm}$ .

Altri esercizi simili:

(Questa pagina è stata visualizzata da 764 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.