Soluzione e svolgimento del seguente problemi di geometria piana.
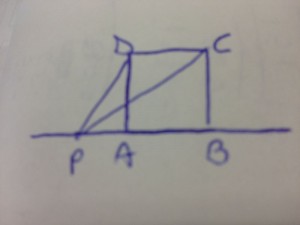
- Dato il quadrato ABCD di lato l, determinare sulla retta AB un punto P tale che la somma dei quadrati delle sue distanze dai vertici C e D sia
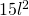
Definendo con ![]() la distanza
la distanza ![]() , otteniamo che:
, otteniamo che:
![]() .
.
Tracciando i segmenti ![]() e
e ![]() , otteniamo due triangoli rettangoli,
, otteniamo due triangoli rettangoli, ![]() e
e ![]() . Dai dati sappiamo che:
. Dai dati sappiamo che:
![]()
Sfruttando il teorema di Pitagora possiamo trovare i valori dei due segmenti:
![]()
![]()
Da qui, sostituendo nella equazione principale, otteniamo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Le soluzioni sono ambedue accettabili perchè, sebbene il valore ![]() risulti essere negativo, questo indica solo la posizione (verso destra o verso sinistra) sulla quale muovere il segmento…
risulti essere negativo, questo indica solo la posizione (verso destra o verso sinistra) sulla quale muovere il segmento…
In parole povere, il punto ![]() , sulla retta
, sulla retta ![]() può distare
può distare ![]() da
da ![]() o
o ![]() da
da ![]() …
…
Altri esercizi simili:
- Esercizi equazioni di secondo grado: Problema 1 di geometria piana
- Esercizi equazioni di secondo grado: Problema 2 di geometria piana
- Esercizi equazioni di secondo grado: Problema 3 di geometria piana
- Esercizi equazioni di secondo grado: Problema 4 di geometria piana
- Esercizi equazioni di secondo grado: Problema 5 di geometria piana
- Esercizi equazioni di secondo grado: Problema 6 di geometria piana
- Esercizi equazioni di secondo grado: Problema 7 di geometria piana
- Esercizi equazioni di secondo grado: Problema 8 di geometria piana
- Esercizi equazioni di secondo grado: Problema 9 di geometria piana
- Esercizi equazioni di secondo grado: Problema 10 di geometria piana
- Esercizi equazioni di secondo grado: Problema 11 di geometria piana
- Esercizi equazioni di secondo grado: Problema 12 di geometria piana
(Questa pagina è stata visualizzata da 579 persone)