Decomporre i seguenti trinomi in fattori di primo grado:
Mettiamo in evidenza il coefficiente della 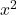 :
:
![]()
quindi dobbiamo trovare due numeri la cui somma faccia ![]() e il prodotto
e il prodotto ![]() .
.
Svolgendo il sistema:
![]()
otteniamo che:
![]()
oppure svolgiamo direttamente l’equazione di secondo grado:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ricordando che, quando le radici sono fratte, il denominatore è il coefficiente della ![]() , otteniamo che:
, otteniamo che:
![]()
Altri hanno visualizzato anche:
- Esercizio 1 Scomposizione del trinomio di secondo grado
- Esercizio 2 Scomposizione del trinomio di secondo grado
- Esercizio 3 Scomposizione del trinomio di secondo grado
- Esercizio 4 Scomposizione del trinomio di secondo grado
- Esercizio 5 Scomposizione del trinomio di secondo grado
- Esercizio 6 Scomposizione del trinomio di secondo grado
- Esercizio 7 Scomposizione del trinomio di secondo grado
- Esercizio 8 Scomposizione del trinomio di secondo grado
- Esercizio 9 Scomposizione del trinomio di secondo grado
- Esercizio 10 Scomposizione del trinomio di secondo grado
(Questa pagina è stata visualizzata da 235 persone)