Radicali

-1

 

Quando parliamo di radicali, intendiamo quella funzione matematica in cui compare un monomio,binomio o polinomio, sotto il segno di radice.

Quindi è facile intuire la definizione di radice n-esima:

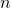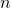  • definiamo radice n-esima di a quel numero x tale per cui, x elevato alla n mi ridà proprio a.
  • \sqrt[n] a= x \Rightarrow x^n=a

Da questa formula ricaviamo che:

  1. \sqrt[n] a è il radicale
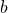  2. b è il coefficiente del radicale
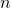  3. n è l’indice della radice
  4. a è il radicando

C’è una differenza tra radicale aritmetico e algebrico: nell’aritmetico non ci interessa sapere il segno del valore ottenuto, nell’algebrico si.

La differenza la notiamo in queste semplici notazioni:

  • radicale aritmetico: \sqrt 9 = |3|
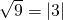
  • radicale algebrico: \sqrt 9 = \pm 3.

 

 

 

 

 

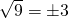Altri hanno visualizzato:

 

(Questa pagina è stata visualizzata da 1447 persone)

Lascia un commento