Traccia
![]()
Svolgimento
Essendo una radice quadrata bisognerà imporre un dominio di esistenza dell’eventuale soluzione dell’equazione, ed imporre anche che il secondo termine sia positivo; quindi svolgeremo un sistema in cui imponiamo che il radicando sia positivo e poi eleveremo al quadrato ambo i membri.
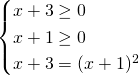
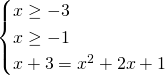
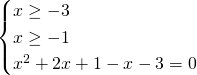
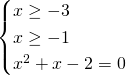
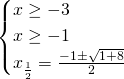
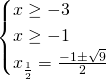
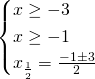
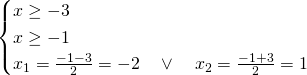
E’ accettabile solo una soluzione, ovvero ![]() .
.
Altri esercizi simili:
- Esercizio 1 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 2 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 3 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 4 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 5 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 6 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 7 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 8 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 9 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 10 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 11 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 12 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 13 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 14 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 15 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 16 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 17 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 18 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 19 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 20 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 21 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 22 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 23 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 24 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 25 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 26 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 27 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 28 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 29 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 30 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 31 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 32 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 33 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 34 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 35 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 36 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 37 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 38 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 39 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 40 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 41 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 42 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 43 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 44 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 45 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 46 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 47 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 48 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 49 Equazioni irrazionali contenenti radicali quadratici 1
- Esercizio 50 Equazioni irrazionali contenenti radicali quadratici 1
(Questa pagina è stata visualizzata da 229 persone)