Sistemi di disequazioni di primo grado

0

In questa situazione affronteremo più disequazioni contemporaneamente. Ogni disequazione va studiata separatamente dalle altre disequazioni.
Si riportano quindi i risultati ottenuti in una tabella contenente solo gli intervalli considerati.
Per ottenere il risultato dobbiamo tenere conto soltanto degli intervalli che soddisfano contemporaneamente tutte le disequazioni presenti.

Da notare anche che un sistema di disequazioni può anche essere privo di soluzioni.

 

Esempio:

\begin{cases} (x-2)(3-x) \leq 0 \\ \frac {2-5x}{4-x} \geq 0 \end{cases}

 

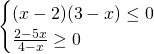
1° Disequazione: (x-2)(3-x) \leq 0

  • x-2 \geq0 \quad x \geq 2
  • 3-x \geq 0 \quad -x \geq -3 \quad x \leq 3
(-\infty;2] [2,3] [3, +\infty)
I —- +++ +++
II +++ +++ —-
—- +++ —-

Risultato della disequazione:

x\leq 2 \quad \lor \quad x \geq 3

 

2° disequazione:  \frac {2-5x}{4-x} \geq 0

  • 2-5x \geq0 \quad -5x \geq -2 \quad x \leq \frac 25
  • 4-x > 0 \quad -x > -4 \quad x < 4
(-\infty;\frac 25] [\frac 25,4) (4, +\infty)
I +++ —- —-
II +++ +++ —-
+++ —- +++

Risultato della disequazione:

x\leq \frac 25 \quad \lor \quad x >4

Quindi, costruendo una tabella contenente tutti i risultati delle due disequazioni, otteniamo:

 

(-\infty; \frac 25] [\frac 25;2] [2;3] [3;4) (4;+\infty)
I +++ +++ +++ +++
II +++ +++
ris +++ +++

 

Da qui si evince che il risultato finale del sistema sarà:

x \leq \frac 25 \quad \lor \quad x>4

oppure

(-\infty; \frac 25] \quad \cup \quad (4;+\infty)

(Questa pagina è stata visualizzata da 535 persone)

Lascia un commento