Esercizio 4 Sistemi di disequazioni di primo grado

-1

\begin{cases} x^2-1 >0 \\ -x+4 \leq 1 \end{cases}

\begin{cases} (x+1)(x-1) >0 \\ x-4 \geq -1 \end{cases}

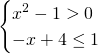
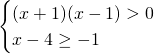
Per risolvere la prima disequazione, basta ricordarsi i casi visti nelle disequazioni riconducibili a quelle di primo grado, dove analizzando singolarmente i 2 casi, e poi mettendoli insieme nel grafico otteniamo questo risultato:

\begin{cases} x<-1 \, \, \lor \, \, x>1 \\ x \geq 4-1 \end{cases}

\begin{cases} x<-1 \, \, \lor \, \, x>1 \\ x \geq 3 \end{cases}

 

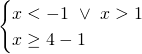
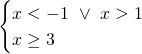
In questo caso le disequazioni sono già risolte, e basterà solo fare il grafico

 

(-\infty; -1) (-1;1) (1;3] [3;+\infty)
I +++ +++ +++
II +++
Risultato +++

 

Si evince facilmente dal grafico che la soluzione sarà:

x \geq 3

oppure

[3;+\infty).

(Questa pagina è stata visualizzata da 250 persone)

Lascia un commento