Esercizio 6 Sistemi di disequazioni di primo grado

-7

\begin{cases} \frac {(x+2)(x-1)}{3} >0 \\ \frac 12 x+1 <0 \end{cases}

\begin{cases} (x+2)(x-1) >0 \\ \frac {x+2}2 <0 \end{cases}

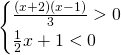
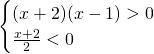
La prima disequazione è riconducibile al primo grado, e, risolvendole singolarmente, otteniamo come risultato:

\begin{cases} x<-2 \, \, \lor \, \, x>1 \\ x+2 <0 \end{cases}

\begin{cases} x<-2 \, \, \lor \, \, x>1 \\ x <-2 \end{cases}

 

 

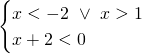
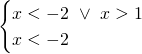
In questo caso le disequazioni sono già risolte, e basterà solo fare il grafico (anche se in realtà abbiamo una sovrapposizione di risultati e il risultato sarebbe immediato…)

 

(-\infty; - 2) (-2;1) (1;+\infty)
I +++ +++
II +++
Risultato +++

 

Si evince facilmente dal grafico che la soluzione sarà:

x < -2

oppure

(-\infty; -2).

(Questa pagina è stata visualizzata da 339 persone)

Lascia un commento