Risoluzione e spiegazione del seguente problema di geometria con due o più incognite
- In un pentagono due angoli consecutivi sono retti; il terzo angolo è i
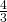 del quinto e supera di
del quinto e supera di 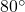 il quarto. Determinare le ampiezze degli angoli.
il quarto. Determinare le ampiezze degli angoli.
Sapendo che la somma degli angoli in un pentagono è ![]() , la somma degli altri 3 angoli sarà di
, la somma degli altri 3 angoli sarà di ![]() . Quindi:
. Quindi:
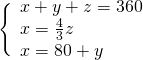
Sostituiamo il risultato della terza nella prima e nella seconda:
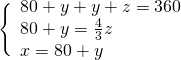
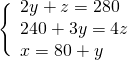
Troviamo ![]() nella prima
nella prima
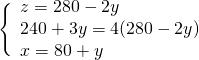
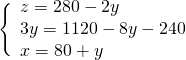
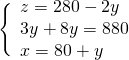
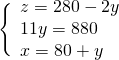
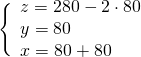
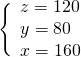
Altri esercizi simili:
- Problema 1 di geometria con due o più incognite
- Problema 2 di geometria con due o più incognite
- Problema 3 di geometria con due o più incognite
- Problema 4 di geometria con due o più incognite
- Problema 5 di geometria con due o più incognite
(Questa pagina è stata visualizzata da 325 persone)