Problemi di primo grado 1

-2

Determinare due numeri sapendo che la differenza fra il primo e i \frac 59 del secondo è 20 e che la somma dei \frac 56 del primo e della terza parte del secondo è 31.

Chiamando con x e y i due numeri, otteniamo le due equazioni:

x-\frac 59 y =20

e

\frac 56 x + \frac 1 3 y=31.

Risolviamo questo sistema:

\Bigg \{ \begin{array}{rl} 9x- 5y = 180 \\ 5 x +2 y = 186 \\ \end{array}

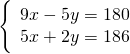
Usiamo il metodo di Cramer:

\Delta= \begin{vmatrix} 9 &-5 \\ 5 & 2 \end{vmatrix}=18+25=43

\Delta_x= \begin{vmatrix} 180 &-5 \\ 186 & 2 \end{vmatrix}= 360+930=1290

\Delta_y= \begin{vmatrix} 9 & 180 \\ 5 & 186 \end{vmatrix}=1674-900=774

x=\frac {\Delta_x}{\Delta}=\frac {1290}{43}=30

y=\frac {\Delta_y}{\Delta}=\frac {774}{43}=18

 

 

Altri hanno visualizzato:

(Questa pagina è stata visualizzata da 281 persone)

Lascia un commento