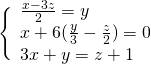
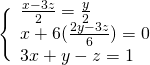
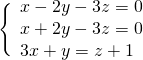
Per velocizzare il tutto, senza dover ogni volta applicare il metodo delle matrici, ci accorgiamo che le prime due equazioni sono molto simili. Quindi facendo la sottrazione membro a membro otteniamo subito che:

.

Il sistema diventa così di due equazioni e due incognite:

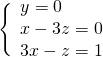
usando il metodo di sostituzione nella seconda otteniamo facilmente le soluzioni:

 

 

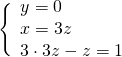
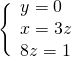
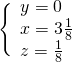
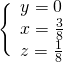
Altri esercizi simili:

• Sistema a più incognite 1
• Sistema a più incognite 2
• Sistema a più incognite 3
• Sistema a più incognite 4
• Sistema a più incognite 5
• Sistema a più incognite 6
• Sistema a più incognite 7
• Sistema a più incognite 8
• Sistema a più incognite 9
• Sistema a più incognite 10

(Questa pagina è stata visualizzata da 226 persone)