Esercizio 3 Sistemi in cui figurano valori assoluti di espressioni contenenti l'incognita

Traccia

$\begin{cases} \left | x \right | -3y = 1-2x \\ x-2y=2 \end{cases}$

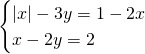
Svolgimento

Avendo il valore assoluto all’interno del sistema, analizzeremo e svolgeremo parallelamente i due sistemi, unendo poi le soluzioni finali.

$\begin{cases} x -3y = 1-2x \\ x-2y=2 \\ x \geq 0 \end{cases} \qquad \begin{cases} -x -3y = 1-2x \\ x-2y=2 \\ x < 0 \end{cases}$

$\begin{cases} 3x -3y = 1 \\ x-2y=2 \\ x \geq 0 \end{cases} \qquad \begin{cases} x -3y = 1 \\ x-2y=2 \\ x < 0 \end{cases}$

$\begin{cases} 3(2+2y)-3y=1 \\ x=2+2y \\ x\geq 0 \end{cases} \qquad \begin{cases} 2+2y-3y=1 \\ x=2+2y \\ x < 0 \end{cases}$

$\begin{cases} 6+6y-3y=1 \\ x=2+2y \\ x\geq 0 \end{cases} \qquad \begin{cases} -y=1-2 \\ x=2+2y \\ x < 0 \end{cases}$

$\begin{cases} 3y=1-6 \\ x=2+2y \\ x\geq 0 \end{cases} \qquad \begin{cases} y=1 \\ x=2+2 \\ x < 0 \end{cases}$

$\begin{cases} y=- \frac 53 \\ x=2+2(-\frac 53) \\ x\geq 0 \end{cases} \qquad \begin{cases} y=1 \\ x=4 \\ x < 0 \end{cases}$

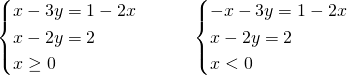
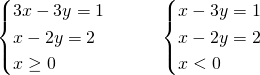
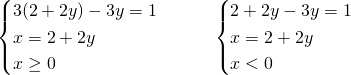
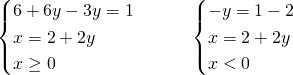
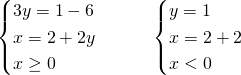
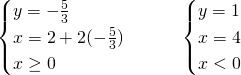
Il secondo sistema è impossibile…

$\begin{cases} y=- \frac 53 \\ x=2-\frac {10}3 \\ x\geq 0 \end{cases}$

$\begin{cases} y=- \frac 53 \\ x=-\frac {4}3 \\ x\geq 0 \end{cases}$

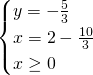
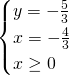
Anche il primo sistema è impossibile, quindi il sistema iniziale non ammetterà soluzione.

Altri esercizi simili:

(Questa pagina è stata visualizzata da 69 persone)

Matebook