Sistema 8

-6

\bigg \{ \begin{array}{ll} 3x+2y=4 \\ 2y-\frac 32(x+3)=-5 \end{array}

\bigg \{ \begin{array}{ll} 3x+2y=4 \\ \frac {4y-3x-9}{2}=\frac {-10}{2} \end{array}

\bigg \{ \begin{array}{ll} 3x+2y=4 \\ 4y-3x=-10+9 \end{array}

\bigg \{ \begin{array}{ll} 3x+2y=4 \\ 4y-3x=-1 \end{array}

 

  • Metodo di sostituzione

Troviamo y nella seconda equazione,  e poi andiamola a sostituire nella prima.

\bigg \{ \begin{array}{ll} 3x+2y=4 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} 3x+2\frac {3x-1}{4}=4 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} 3x+\frac {3x-1}{2}=4 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} \frac {6x + 3x-1}{2}=\frac 8 2 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} 9x = 8+1 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} x= \frac {9}{9}= 1 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} x= 1 \\ y=\frac {3(1)-1}{4} \end{array}

\bigg \{ \begin{array}{ll} x= 1 \\ y=\frac {1}{2} \end{array}

 

  • Metodo di confronto

Troviamo y in entrambe le equazioni, così da risolvere poi un’equazione di primo grado con incognita x e teniamo solo la seconda.

\bigg \{ \begin{array}{ll} y=\frac {4-3x} 2 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} \frac {4-3x} 2=\frac {3x-1}4 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} \frac {8-6x} 4=\frac {3x-1}4 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} -6x -3x=-1-8 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} 9x = 9 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} x= \frac {9}{9}= 1 \\ y=\frac {3x-1}{4} \end{array}

\bigg \{ \begin{array}{ll} x= 1 \\ y=\frac {3(1)-1}{4} \end{array}

\bigg \{ \begin{array}{ll} x= 1 \\ y=\frac {1}{2} \end{array}

 

 

 

  • Metodo di eliminazione

Eseguiamo la somma membro a membro, lasciando la seconda equazione così com’è.

\bigg \{ \begin{array}{ll} 2y +4y = 4-1 \\ x=\frac {4y+1}{3} \end{array}

\bigg \{ \begin{array}{ll} 6y=3 \\ x=\frac {4y+1}{3} \end{array}

\bigg \{ \begin{array}{ll} y= \frac 3 6 = \frac 1 2 \\ x=\frac {4y+1}{3} \end{array}

\bigg \{ \begin{array}{ll} y= \frac 1 2 \\ x=\frac {4(\frac 1 2 )+1}{3} \end{array}

\bigg \{ \begin{array}{ll} y= \frac 1 2 \\ x=1 \end{array}

 

 

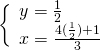
Altri esercizi simili

(Questa pagina è stata visualizzata da 412 persone)

Lascia un commento