Esercizio 1 Sistemi di equazioni di grado superiore al primo: 2 equazioni in 2 incognite

Traccia

$\begin{cases} x-y=3 \\ x^2-2xy+3y=11 \end{cases}$

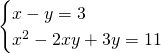
Svolgimento

$\begin{cases} x=3+y \\ (3+y)^2-2y(3+y)+3y=11 \end{cases}$

$\begin{cases} x=3+y \\ 9+6y+y^2-6y-2y^2+3y=11 \end{cases}$

$\begin{cases} x=3+y \\ -y^2 +3y-2=0 \end{cases}$

$\begin{cases} x=3+y \\ y^2 -3y +2=0 \end{cases}$

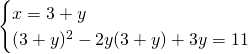
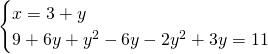
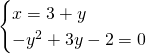
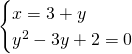
Svolgiamo l’equazione di secondo grado per trovare le 2 soluzioni:

$y_{\frac 12}= \frac {3\pm \sqrt {9-8}}{2}$

$y_{\frac 12}= \frac {3\pm \sqrt {1}}{2}$

$y_{\frac 12}= \frac {3\pm 1}{2}$

$y_1= \frac {3 - 1}{2}=\frac 22=1$

$y_2= \frac {3 + 1}{2}=\frac 42 =2$

Quindi le due coppie di soluzioni saranno:

$\begin{cases} x=4 \\ y=1 \end{cases} \qquad \begin{cases} x=5 \\ y=2 \end{cases}$

Altri esercizi simili:

(Questa pagina è stata visualizzata da 95 persone)

Matebook