Esercizio 3 Sistemi simmetrici di secondo grado

0

Traccia

\begin{cases} x+y=2 \\ xy=1 \end{cases}

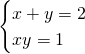
Svolgimento

Essendo un sistema simmetrico possiamo considerare le due incognite come se fossero le radici di un’equazione di secondo grado e quindi trovare le soluzioni semplicemente svolgendo:

t^2-2t+1=0

t_{\frac 12}= \frac {2 \pm \sqrt {4-4}}{2}

t_{\frac 12}= \frac {2 \pm \sqrt {0}}{2}

t_{\frac 12}= \frac {2 \pm 0}{2}

t_1= \frac { 2-0}{2}=1

t_2= \frac {2 + 0}{2}=1

Quindi le due coppie di risultati saranno:

\begin{cases} x=1 \\ y= 1 \end{cases} \quad \lor \quad \begin{cases} x= 1 \\ y=1 \end{cases}

 

 

 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 128 persone)

Lascia un commento