Data una funzione ![]() definita in un insieme
definita in un insieme ![]() (in realtà andrebbe incluso uguale)!!!, questa si dice:
(in realtà andrebbe incluso uguale)!!!, questa si dice:
- pari se
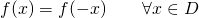
- dispari se
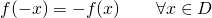
Un esempio di funzione pari è ![]() , ove l’ordinata ottenuta sostituendo
, ove l’ordinata ottenuta sostituendo ![]() è uguale all’ordinata ottenuta sostituendo
è uguale all’ordinata ottenuta sostituendo ![]() ; una funzione pari è sempre simmetrica rispetto all’asse delle
; una funzione pari è sempre simmetrica rispetto all’asse delle ![]() .
.
Es.
![]()
![]()
Un esempio di funzione dispari è ![]() , dove l’ordinata ottenuta sostituendo
, dove l’ordinata ottenuta sostituendo ![]() è opposta all’ordinata ottenuta sostituendo
è opposta all’ordinata ottenuta sostituendo ![]() ; una funzione dispari è sempre simmetrica rispetto all’origine.
; una funzione dispari è sempre simmetrica rispetto all’origine.
Es.
![]()
![]()
(Questa pagina è stata visualizzata da 269 persone)