Esercizio 6 Problemi sul teorema di Talete e le sue applicazioni

Traccia

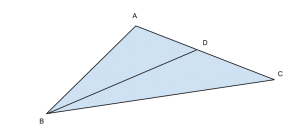
Nel triangolo ABC sia BD la bisettrice dell’angolo in B. Si sa che AB=91a, che CB supera di 18a il doppio di DC e che AD-DC=5a. Determinare la misura del perimetro di ABC. Quante soluzioni ha il problema?

Svolgimento

Dai dati, ponendo $CD=x$ , abbiamo:

$AB=91a$

$CB=2x+18a$

$AD=5a+x$

$AC=5a+2x$

Dal teorema della bisettrice, sappiamo che:

$\frac {AB}{AD}=\frac {CB}{DC}$

o meglio:

$CB\cdot AD=AB \cdot DC$

$(2x+18a)(5a+x)=91ax$

$2x^2+10ax+18ax+90a^2-91ax=0$

$2x^2-63ax+90a^2=0$

$(2x-3a)(x-30a)=0$

Quindi ammetterà due soluzioni:

$x_1=\frac 32 a\, \, \mbox { o } x_2= 30a$

Con

$DC=\frac 32a$

$CB=21a$

$AC=8a$

$2p=8a+21a+91a=120a$

Con

$DC=30a$

$CB=78a$

$AC=65a$

$2p=65a+78a+91a=234a$

In base a questi due risultati, possiamo escludere la prima soluzione in quanto, in un triangolo, il perimetro deve essere maggiore di 2 volte un qualsiasi lato del triangolo ( $120a < 2 \cdot 91a=182a$ ), e quindi diventa accettabile solo la seconda.

Altri esercizi simili:

(Questa pagina è stata visualizzata da 237 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.