Esercizio 11 Problemi su triangoli e poligoni simili

-2

Traccia

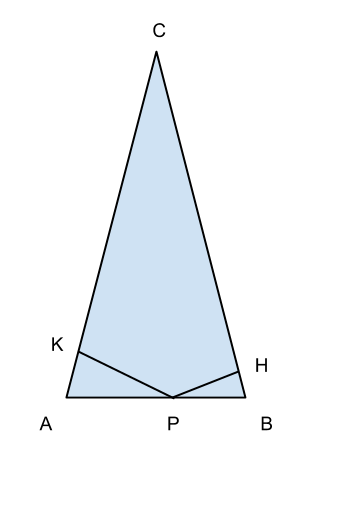
Il perimetro di un triangolo ABC, isoscele sulla base AB, è 144 cm e il lato BC supera la base di 12 cm. Determinare i tre lati.  Dal punto P di AB tale che AP=7/13 PB si conducano le perpendicolari PH e PK rispettivamente ai lati BC e AC. Determinare il perimetro dei triangoli AKP e PHB.

Svolgimento

tr iso

Chiamiamo AB=x, e avremo:

AC=BC=12+x

2p=AB+BC+AC=x+12+x+12+x=3x+24=144 \mbox { cm}

da cui avremo:

3x=120

x=40

Quindi:

AB=40 \mbox { cm}

AC=BC=52 \mbox { cm}.

Calcoliamo ora AP e PB, sapendo che:

AP=\frac {7}{13}PB

AB=AP+PB=\frac {7}{13}PB+PB=\frac {20}{13}PB=40 \mbox { cm}

Da qui avremo che:

PB=26\mbox { cm}

AP=14\mbox { cm}

Troviamo anche la lunghezza dell’altezza CM che ci servirà tra un attimo, con il teorema di Pitagora:

CM=\sqrt {AC^2-(\frac12AB)^2}=\sqrt {2704-400} \mbox { cm}=\sqrt {2304}\mbox { cm}=48\mbox { cm}

Dal disegno si evince che, tracciando l’altezza CM, i triangoli AMC, APK e PBH sono simili, avendo ognuno un angolo in comune ed essendo retti.

Con i criteri di proporzionalità ricaviamo adesso i lati:

AK:AP=AM:AC

AK=\frac {AP \cdot AM}{AC}=\frac {14 \cdot 20}{52}\mbox { cm}=\frac {70}{13}\mbox { cm}

PK:AP=CM:AC

PK=\frac {AP \cdot CM}{AC}=\frac {14 \cdot 48}{52}\mbox { cm}=\frac {168}{13}\mbox { cm}

Troviamo quindi il perimetro:

2p_{APK}=(14+\frac {70}{13}+\frac {168}{13})\mbox { cm}=\frac {420}{13}\mbox { cm}

BH:BP=BM:BC

BH=\frac {BP \cdot BM}{BC}=\frac {26 \cdot 20}{52}\mbox { cm}=10\mbox { cm}

PH:BP=CM:BC

PH=\frac {BP \cdot CM}{BC}=\frac {26 \cdot 48}{52}\mbox { cm}=24\mbox { cm}

Troviamo quindi il perimetro:

2p_{PBH}=(26+10+24)\mbox { cm}=60\mbox { cm}


 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 66 persone)

Lascia un commento