Esercizio 14 Problemi su triangoli e poligoni simili

Traccia

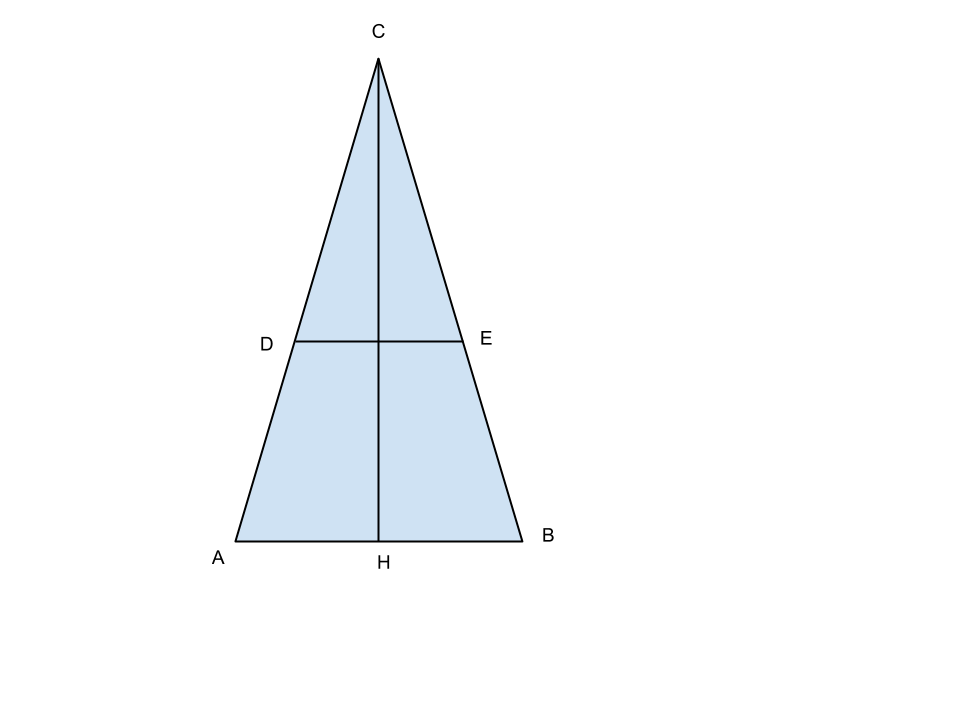
Il perimetro del triangolo isoscele ABC è di 384 cm e la base AB è i 14/25 del lato AC. Determinare la lunghezza della corda DE parallela alla base AB in modo che il perimetro del trapezio ABED sia di 240 cm.

Svolgimento

Dalla traccia abbiamo che:

$2p_{ABC}=384 \mbox { cm}$

$AB=\frac {14}{25}AC$

Sfruttiamo questi due dati per ricavare i lati:

$2p=AB+AC+BC=\frac {14}{25}AC+AC+AC=\frac {64}{25}AC=384 \mbox { cm}$

Quindi avremo che:

$AC=150 \mbox { cm}$

$AB=84\mbox { cm}$ .

Notiamo che i due triangoli CDE e ABC sono simili, e di conseguenza, vale il rapporto:

$DE:AB=DC:AC$

$DE=\frac {AB \cdot DC}{AC}=\frac {14}{25}DC$ .

Ora il nostro scopo è trovare DC.

sappiamo che il perimetro di ABDE sarà, ponendo $DC=CE=x$

$2p_{ABDE}=AB+BE+ED+DA$

$84 +150-x+\frac {14}{25}x +150-x=240$

$-\frac {36}{25}x=240-384$

$x=\frac {25}{36}144=100$

Trovato $DC=100 \mbox { cm}$ , ricaviamo

$DE=\frac {14}{25}DC=\frac {14}{25}100 \mbox { cm}=56 \mbox { cm}$ .

Altri esercizi simili:

(Questa pagina è stata visualizzata da 123 persone)

Matebook

La matematica spiegata passo passo

Esercizio 14 Problemi su triangoli e poligoni simili

Lascia un commento Annulla risposta