Esercizio 16 Problemi su triangoli e poligoni simili

-1

Traccia

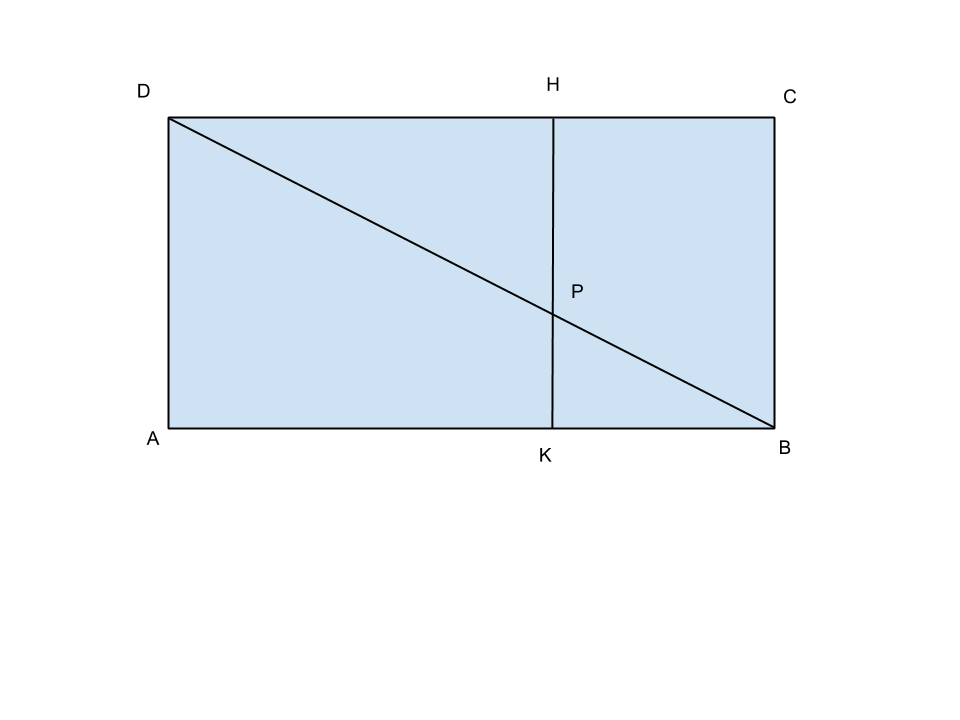
Del rettangolo ABCD si conoscono AB=48 cm e AD=36 cm; sia P il punto della diagonale BD tale che sia DP=1/6 BD. Da P di conduca la parallela ad AD e si indichino con H e K le intersezioni di tale parallela rispettivamente con AB e con CD. Individuare tutti i triangoli simili al triangolo ABD. Determinare poi l’area del quadrilatero BCPH.

Svolgimento

rettangolo con diagonale

I triangoli simili con il triangolo ABD sono:

PHB, PKD, CBD.

Ricaviamo ora la diagonale BD con il teorema di Pitagora:

DB=\sqrt{ DA^2+AB^2} =\sqrt { 1296 + 2304}\mbox { cm} =\sqrt { 3600} \mbox { cm}= 60 \mbox { cm}

Dalla traccia sappiamo anche che:

DP=\frac 16 DB=10 \mbox { cm}

BP=DB-DP=50\mbox { cm}.

Ora, come si nota, il quadrilatero BCPH è un trapezio rettangolo, quindi ci basterà ricavare BH e PH.

Dalle similitudini dei triangoli avremo che:

HB:AB=PB:DB

HB=\frac {AB \cdot PB}{DB}=\frac {48 \cdot 50}{60}\mbox { cm}=40 \mbox { cm}

PH:AD=PB:DB

PH=\frac {AD \cdot PB}{DB}=\frac {36 \cdot 50}{60}\mbox { cm}=30 \mbox { cm}

A_{BCPH}=\frac {(BC+PH)\cdot BH}{2}=\frac {(36+30) \cdot 40}{2}\mbox { cm}^2=1320 \mbox { cm}^2

 

 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 114 persone)

Lascia un commento