Esercizio 17 Problemi su triangoli e poligoni simili

-1

Traccia

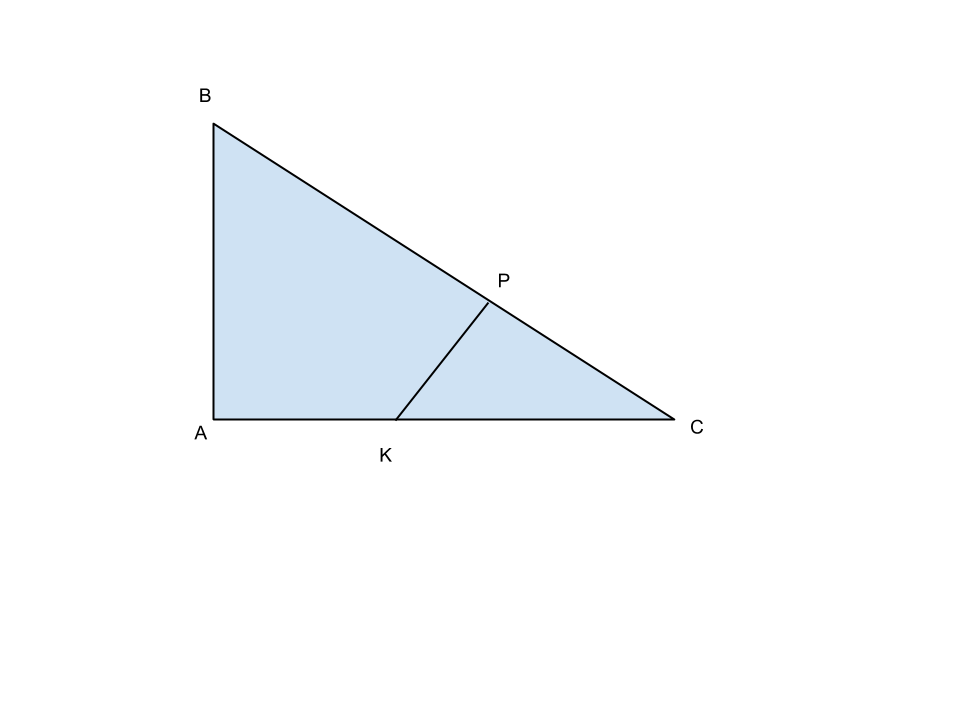
Nel triangolo rettangolo ABC l’ipotenusa BC è i 5/3 del cateto AB e il perimetro è lungo 72 cm. Da un punto P dell’ipotenusa  che, a partire dal vertice C, la divide in parti proporzionali ai numeri 3 e 7 si conduca la perpendicolare all’ipotenusa. Determinare il perimetro e l’area delle due parti in cui resta diviso il triangolo.

Svolgimento

triangolo rettangolo ipotenusa

Ricaviamo subito i lati, ponendo AB=x, così da avere:

BC=\frac 53x

e ricavare AC con il teorema di Pitagora:

AC=\sqrt {BC^2-AB^2}=\sqrt {\frac {25}{9}x^2-x^2}=\sqrt {\frac {16}{9}x^2}=\frac 43x

Imponendo la relazione del perimetro, ricaviamo l’incognita:

x+\frac 53x+ \frac 43x=72 \mbox { cm}

\frac {12}{3}x=72 \mbox { cm}

x=18 \mbox { cm}.

Da cui:

AB=18 \mbox { cm}

BC=30 \mbox { cm}

AC=24 \mbox { cm}.

Dalla traccia sappiamo che:

PC =\frac 37 BP

BC=BP+PC=BP+\frac 37BP=\frac {10}{7}BP.

Ricaviamo i due segmenti:

BP=\frac {7}{10}BC=21 \mbox { cm}

CP=BC-BP=9 \mbox { cm}

Per costruzione sappiamo anche che i due triangoli ABC e KPC sono simili e usiamo quindi il criterio di proporzionalità sui lati:

CK:BC=CP:AC

CK=\frac {BC \cdot CP}{AC}=\frac {30 \cdot 9}{24} \mbox { cm}=\frac {45}{4} \mbox { cm}

AK=AC-CK=(24-\frac {45}{4})\mbox { cm}=\frac {51}{4}\mbox { cm}

PK:AB=CP:AC

PK=\frac {AB \cdot CP}{AC}=\frac {18 \cdot 9}{24} \mbox { cm}=\frac {27}{4} \mbox { cm}

BP=BC-PC=(30-9)\mbox { cm}=21\mbox { cm}.

Calcoliamo ora i perimetri:

2p_{KPC} = PC + PK + KC = (9 + \frac {27}{4} + \frac {45}{4}) \mbox { cm}= 27 \mbox { cm}

2p_{ABPK} = AB + BP + PK + KA = (18 + 21 + \frac {27}{4} + \frac {51}{4})\mbox { cm} = \frac {234}{4}\mbox { cm}=\frac {117}{2}\mbox { cm}.

Ricaviamo ora le 2 aree:

A_{ABC} = \frac {AB \cdot AC}{2} = \frac {18 \cdot 24}{2} = 216 \mbox { cm}^2.
A_{KPC} = \frac {KP \cdot PC}{2} = \frac {243}{8} \mbox { cm}^2.
A_{ABPE} =A_{ABC} -A_{EPC} = (216 - \frac {243}{8}) \mbox { cm}^2= \frac {1485}{8}\mbox { cm}^2


 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 57 persone)

Lascia un commento