Esercizio 27 Problemi su triangoli e poligoni simili

-1

Traccia

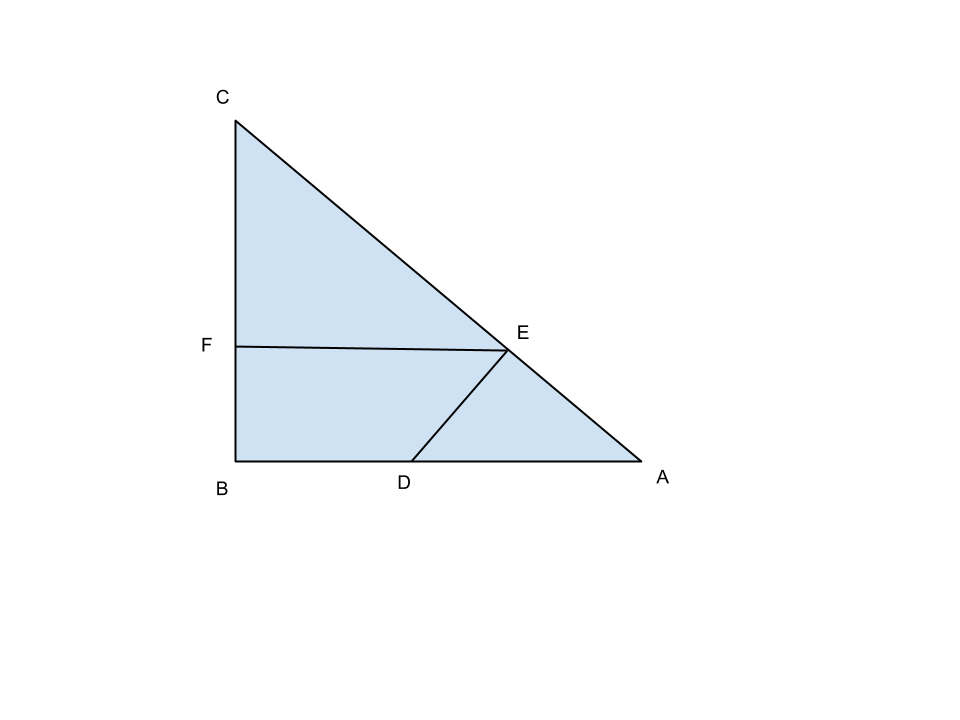
I cateti AB e BC del triangolo rettangolo ABC sono rispettivamente 12 e 16 cm. Determinare un punto D sul cateto AB in modo che sia verificata la relazione seguente

    \[\frac {CE^2-DE^2}{EF\cdot AD - AE \cdot DE}=7\]

, essendo E la proiezione ortogonale di D sull’ipotenusa AC ed F la proiezione di E sul cateto BC.

Svolgimento

triangolo con proiezioni

Per prima cosa troviamo l’ipotenusa AC con il teorema di Pitagora:

BC=\sqrt {AB^2+BC^2}=\sqrt {144+256}\mbox { cm}=\sqrt {400} \mbox{ cm}=20\mbox{ cm}.

Poniamo EC=y \, \, e \, \, AE=x, e, notando che i triangoli ADE, EFC e ABC sono simili otteniamo:

AD:AC=AE:AB

AD=\frac {AC\cdot AE}{AB}=\frac {20y}{12}=\frac 53y

Allo stesso modo troviamo DE:

DE:BC=AE:AB

DE=\frac {BC\cdot AE}{AB}=\frac {16y}{12}=\frac 43y

EF:AB=CE:AC

EF=\frac {AB \cdot CE}{AC}=\frac {12x}{20}=\frac 35x.

Sostituiamo tutto nella condizione richiesta dalla traccia:

\frac {CE^2-DE^2}{EF\cdot AD - AE \cdot DE}=7

\frac {x^2-(\frac 43y)^2}{\frac 35x \frac 53y -y \frac 43y}=7

\frac {(x+\frac 43y)(x-\frac 43y)}{xy - \frac 43y^2}=7

\frac {(x+\frac 43y)(x-\frac 43y)}{y(x - \frac 43y)}=7

Imponendo come condizione di esistenza che x \neq \frac 43y, otteniamo:

x+\frac 43y=7y

x=\frac {17}{3}y

Ora per costruzione, sappiamo che:

x+y=20

\frac {17}{3}y+y=20

y=3

E quindi, il segmento AD sarà:

AD=\frac 53y=5 \mbox { cm}.


 

 

 

Altri esercizi simili:

 

(Questa pagina è stata visualizzata da 112 persone)

Un pensiero riguardo “Esercizio 27 Problemi su triangoli e poligoni simili”

Lascia un commento