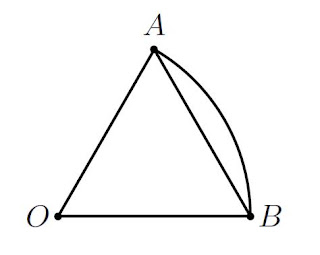
Viene assegnato il settore circolare AOB di raggio r e ampiezza x (r e x sono misurati, rispettivamente, in metri e radianti).
1. Si provi che l’area S compresa fra l’arco e la corda AB è espressa, in funzione di x, da
![\[S(x)=\frac 12 r^2(x−sinx) \quad \quad x \in \left[0,2 \pi \right].\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-1a661a3e8341f1c935209e4e8fcb6ea1_l3.png "Rendered by QuickLaTeX.com")
2. Posto 
, si studi come varia S e se ne disegni il grafico.
3. Si fissi l’area del settore AOB pari a 100 metri quadri. Si trovi il valore di r per il quale è minimo il perimetro di AOB e si esprima il corrispondente valore di x in gradi sessagesimali (è sufficiente l’approssimazione al grado).
4. Sia
![\[r=2 \quad \mbox{ e } x=\frac {\pi}{3}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-4fb3fb2538140b54e367a1bed4905420_l3.png "Rendered by QuickLaTeX.com")
. Il settore AOB è la base di un solido W le cui sezioni ottenute con piani ortogonali ad OB sono tutte quadrati. Si calcoli il volume di W.
Altri esercizi simili:
(Questa pagina è stata visualizzata da 4 persone)