Problema 2.4 PNI 2010

0

Problema 2

 

Nel piano riferito ad un sistemaOxy di coordinate cartesiane siano assegnate le parabole di equazioni: y^2=2x e x^2=y

 

4. Si consideri il solido W ottenuto dalla rotazione di D intorno all’asse x. Se si taglia W con piani ortogonali all’asse x, quale forma hanno le sezioni ottenute? Si calcoli il volume di W.

 

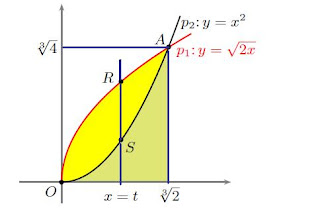
La rotazione di D attorno all’asse x genera il solido in figura dove la superficie esterna appare quella di un paraboloide (che è la superficie che si ottiene dalla rotazione di una parabola attorno al proprio asse di simmetria). Le sezioni di questo solido con piani perpendicolari all’asse x si possono individuare anche riprendendo la regione D e considerando le sue sezioni bidimensionali ottenute con il fascio di rette x =t quando sia

    \[0\let\le\sqrt[3]2\]

Il volume di W si può calcolare come differenza di due solidi: quello generato dalla regione delimitata dalla parabola p_1, dall’asse x e dalla retta x=\sqrt[3]2, con quello, più interno, generato dalla rotazione della regione definita dall’arco di p_2, dall’asse x e dalla retta precedentemente descritta.

    \[V_1=\pi \int_0^{\sqrt[3]2} \left(\sqrt{2x}\right)^2 dx=\pi \int_0^{\sqrt[3]2} 2x dx\]

    \[V_2=\pi \int_0^{\sqrt[3]2} \left(x^2\right)^2 dx=\pi \int_0^{\sqrt[3]2} x^4 dx\]

    \[V(W)=V_1−V_2=\pi \int_0^{\sqrt[3]2} 2x dx- \pi \int_0^{\sqrt[3]2} x^4 dx=\ldots = \frac 35 \pi \sqrt[3]4\]

 

 

Altri esercizi simili:

 

(Questa pagina è stata visualizzata da 2 persone)

Lascia un commento