Siano ABC un triangolo rettangolo in A, r la retta perpendicolare in B al piano del triangolo e P un punto di r distinto da B. Si dimostri che i tre triangoli PAB, PBC, PCA sono triangoli rettangoli.

 

Essendo r perpendicolare in B al piano ABC, r è perpendicolare a tutte le rette di tale piano passanti per B.

Ne segue che:

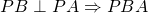• è rettangolo in B
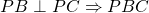• è rettangolo in B.

Per quanto riguarda il triangolo PAC, per il teorema delle tre perpendicolari, AC è perpendicolare in A al piano PAB; in particolare è perpendicolare a PA. Ne segue che anche il triangolo PAC è rettangolo in A.

 

 

Altri esercizi simili

• Quesito 1 PNI 2010
• Quesito 2 PNI 2010
• Quesito 3 PNI 2010
• Quesito 4 PNI 2010
• Quesito 5 PNI 2010
• Quesito 6 PNI 2010
• Quesito 7 PNI 2010
• Quesito 8 PNI 2010
• Quesito 9 PNI 2010
• Quesito 10 PNI 2010

(Questa pagina è stata visualizzata da 5 persone)