Problema 1 P.N.I. 2011

Sia $f$ la funzione definita sull’insieme R dei numeri reali da $f(x)= x + ln 4 + \frac {2}{e^x+1}$ e sia $\Gamma$ la sua rappresentazione grafica nel sistema di riferimento $Oxy$ .

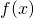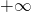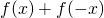Si determini il limite di $f(x)$ per x che tende a $+\infty$ e a $-\infty$ . Si calcoli $f(x) + f(-x)$ e si spieghi perchè dal risultato si può dedurre che il punto 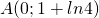$A(0; 1 + ln4)$ è centro di simmetria di $\Gamma$ .
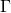Si provi che, per tutti i reali m, l’equazione 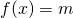$f(x) = m$ ammette una e una sola soluzione in R. Sia 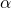$\alpha$ la soluzione dell’equazione 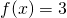$f(x) = 3$ ; per quale valore di m il numero 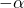$-\alpha$ è soluzione dell’equazione $f(x ) = m$ ?
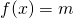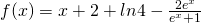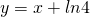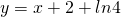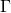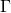Si provi che, per tutti gli x reali, è: $f(x) = x + 2+ ln 4 -\frac {2e^x}{e^x+1}$ . Si provi altresì che la retta r di equazione $y = x + ln4$ e la retta s di equazione $y = x + 2 + ln 4$ sono asintoti di $\Gamma$ e che $\Gamma$ è interamente compresa nella striscia piana delimitata da r e da s.
Posto $I(\beta)=\int_0^{\beta} \left [(f(x)-x-ln 4 \right] dx$ , si calcoli:
$\lim_{\beta \to +\infty}I(\beta).$

Qual è il significato geometrico del risultato ottenuto?

Altri esercizi simili

(Questa pagina è stata visualizzata da 41 persone)

Matebook

La matematica spiegata passo passo

Problema 1 P.N.I. 2011

Lascia un commento Annulla risposta