Problema 1.4 Scientifico 2011

0

Si considerino le funzioni  f e g definite, per tutti gli x reali, da:

    \[f (x) = x^3 - 4x \quad \quad \mbox { e } \quad \quad g (x) = sen (\pi x).\]

 

 

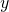  • La regione R rappresenta la superficie libera dell’acqua contenuta in una vasca. In ogni punto di R a distanza x dall’asse y la misura della profondità dell’acqua nella vasca è data da 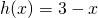h(x) = 3 - x. Quale integrale definito dà il volume dell’acqua? Supposte le misure in metri, quanti litri di acqua contiene la vasca?

Per calcolare il volume richiesto, basterà notare che le sezioni di acqua saranno dei rettangoli di base g(x)-f(x) e di altezza h(x).

Quindi avremo:

    \[V= \int_0^2 (g(x)-f(x))\cdot h(x) dx= \int_0^2 (sen \pi x - x^3+4x)(3-x)dx=\]

    \[=\int_0^2 (3sen \pi x -3x^3+12x-xsen \pi x +x^4 -4x^2) dx=\int_0^2 ((3-x)sen \pi x +x^4-3x^3-4x^2+12x)dx.\]

Visto che gli integrali dei polinomi sono immediati, calcoliamo l’integrale particolare presente per parti:

    \[\int (3-x)sen \pi x dx\]

f'(x) = sen \pi x \Rightarrow f(x)= -\frac {1}{\pi} cos \pi x

g(x)=3-x \Rightarrow g'(x)= -1.

Avremo quindi:

    \[\int (3-x)sen \pi x dx= (3-x)\left(-\frac {cos \pi x}{\pi}\right)- \int -1 \cdot \left (-\frac {cos \pi x}{\pi} \right) dx= (x-3)\frac {cos \pi x}{\pi}-\frac {sen \pi x}{\pi^2}+c.\]

Ritorniamo al calcolo precedente e otterremo:

    \[V=\left[\frac {(x-3)cos \pi x}{\pi}-\frac {sen \pi x}{\pi^2}+\frac {x^5}{5}-\frac 34 x^4-\frac 43 x^3+6x^2 \right]_0^2=\]

    \[=\frac {-cos 2\pi}{\pi}-0+\frac {32}{5}-12-\frac {32}{2}+24-\left(-\frac {3}{\pi}-0\right)=\]

    \[=-\frac {1}{\pi}+ \frac {32}{5}-\frac {32}{3}+12+\frac {3}{\pi}=\frac {2}{\pi}+ \frac {116}{15}\simeq 8,37\]

Dato che il risultato deve essere in metri cubi, avremo che la vasca contiene circa 8370 l d’acqua.

 
 

Altri esercizi simili

 

(Questa pagina è stata visualizzata da 10 persone)

Lascia un commento