Problema 2.1 P.N.I. 2011

Per il progetto di una piscina, un architetto si ispira alle funzioni f e g definite, per tutti gli x reali, da:

$f(x) = x^3 - 16x \quad \quad \mbox { e } \quad \quad g(x)= sen \frac {\pi}{2} x.$

Si studino le funzioni $f$ e $g$ e se ne disegnino i rispettivi grafici in un conveniente sistema di riferimento cartesiano $Oxy$ . Si considerino i punti del grafico di $g$ a tangente orizzontale la cui ascissa è compresa nell’intervallo [–10; 10] e se ne indichino le coordinate.

Studiamo $f(x)$ :

Essendo una funzione razionale intera, il dominio sarà proprio l’insieme dei numeri reali, quindi $D=R$ .

Essendo una funzione polinomiale con termini di grado dispari, allora ovviamente sarà dispari, infatti:

$f(-x)=-x^3+16x=-f(x)=$ .

Intersecherà l’origine degli assi, e:

$\begin {cases} y=0 \\ x(x^2-16)=0\end{cases}$

$\begin {cases} y=0 \\ x(x-4)(x+4)=0\end{cases}$

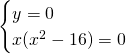
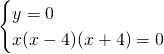
Quindi intersecherà gli assi nei punti:

$o(0;0) \quad A(4;0) \quad B(-4;0)$ .

La funzione $f(x)=x^3-16x$ sarà positiva se $x(x+4)(x-4)>0$ , e quindi sarà positiva per $-4<x<0$ e per $x>4$ , e negativa per $x<-4$ e per $0<x<4$ .

I limiti agli estremi del dominio saranno:

$\lim_{x \to \pm \infty}f(x)=\pm \infty$ .

ed ovviamente, essendo una funzione polinomiale, questa non ammette asintoti.

Studiamo la derivata prima:

$f'(x)=3x^2-16$

Quindi la derivata prima sarà positiva (f crescente)per $x<- \frac {4}{\sqrt 3}$ e per $x>\frac {4}{\sqrt 3}$ , e negativa (f decrescente) per $-\frac {4}{\sqrt 3}<x<\frac {4}{\sqrt 3}$ .

Ammetterà un massimo in $\left(-\frac {4}{\sqrt 3};\frac {128}{3\sqrt 3}\right)$ e un minimo in $\left(\frac {4}{\sqrt 3};-\frac {128}{\sqrt 3}\right)$ .