Siano ![]() e
e ![]() le funzioni definite, per tutti gli x reali, da
le funzioni definite, per tutti gli x reali, da
![]()
- Qual è il periodo della funzione
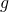 ? Si studino
? Si studino 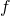 e
e 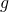 e se ne disegnino i rispettivi grafici
e se ne disegnino i rispettivi grafici 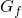 e
e 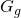 in un conveniente sistema di riferimento cartesiano
in un conveniente sistema di riferimento cartesiano 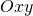 .
. - Si scrivano le equazioni delle rette
 e
e  tangenti, rispettivamente, a
tangenti, rispettivamente, a 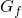 e a
e a 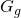 nel punto di ascissa
nel punto di ascissa 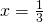 . Qual è l’ampiezza, in gradi e primi sessagesimali, dell’angolo acuto formato da
. Qual è l’ampiezza, in gradi e primi sessagesimali, dell’angolo acuto formato da  e da
e da  ?
? - Sia R la regione delimitata da
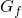 e da
e da 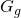 . Si calcoli l’area di R.
. Si calcoli l’area di R. - La regione R, ruotando attorno all’asse x, genera il solido S e, ruotando attorno all’asse y, il solido T. Si scrivano, spiegandone il perchè, ma senza calcolarli, gli integrali definiti che forniscono i volumi di S e di T.
Altri esercizi simili
- Problema 1 P.N.I. 2012
- Problema 1 Scientifico 2012
- Problema 2 P.N.I. 2012
- Problema 2 Scientifico 2012
- Quesiti P.N.I. 2012
- Quesiti Scientifico 2012
(Questa pagina è stata visualizzata da 25 persone)