Nel primo quadrante del sistema di riferimento sono assegnati l’arco di circonferenza di centro O e estremi A(3, 0) e B(0, 3) e l’arco L della parabola d’equazione i cui estremi sono il punto A e il punto (0, 3/2).

 

1. Sia la retta tangente in A a L. Si calcoli l’area di ciascuna delle due parti in cui divide la regione R racchiusa tra L e l’arco AB.
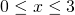2. La regione R è la base di un solido W le cui sezioni, ottenute tagliando W con piani perpendicolari all’asse , hanno, per ogni , area 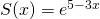. Si determini il volume di W.
3. Si calcoli il volume del solido ottenuto dalla rotazione di R intorno all’asse .
4. Si provi che l’arco L è il luogo geometrico descritto dai centri delle circonferenze tangenti internamente all’arco AB e all’asse x. Infine, tra le circonferenze di cui L è il luogo dei centri si determini quella che risulta tangente anche all’arco di circonferenza di centro A e raggio 3, come nella figura a lato.

 

 

 

 

Altri esercizi simili

• Problema 1 P.N.I. 2012
• Problema 1 Scientifico 2012
• Problema 2 P.N.I. 2012
• Problema 2 Scientifico 2012
• Quesiti P.N.I. 2012
• Quesiti Scientifico 2012

(Questa pagina è stata visualizzata da 20 persone)