Quesiti P.N.I. 2012

0
  1. Si calcoli

        \[\lim_{x \to 0^+} \frac {2^{3x}-3^{4x}}{x^2}\]

  2. Una moneta da 1 euro (il suo diametro è 23,25 mm) viene lanciata su un pavimento ricoperto con mattonelle esagonali (regolari) di lato 10 cm. Quale è la probabilità che la moneta vada a finire internamente ad una mattonella (cioè non tagli i lati degli esagoni)?
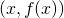  3. Sia f (x)=3^x . Per quale valore di x, approssimato a meno di 10^{-3}, la pendenza della retta tangente alla curva nel punto(x, f (x)) è uguale a 1?
  4. L’insieme dei numeri naturali e l’insieme dei numeri razionali sono insiemi equipotenti? Si giustifichi la risposta.
  5. Siano dati nello spazio n punti P1, P2, P3, …. Pn . Quanti sono i segmenti che li congiungono a due a due? Quanti i triangoli che hanno per vertici questi punti (supposto che nessuna terna sia allineata)? Quanti i tetraedri (supposto che nessuna quaterna sia complanare)?
  6. Si dimostri che la curva di equazione 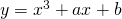y=x^3+  ax+ b ha uno ed un solo punto di flesso rispetto a cui è simmetrica.
  7. E’ dato un tetraedro regolare di spigolo l e altezza h. Si determini l’ampiezza dell’angolo α formato da l e da h.
  8. Un’azienda industriale possiede tre stabilimenti (A, B e C). Nello stabilimento A si produce la metà dei pezzi, e di questi il 10% sono difettosi. Nello stabilimento B si produce un terzo dei pezzi, e il 7% sono difettosi. Nello stabilimento C si producono i pezzi rimanenti, e il 5% sono difettosi. Sapendo che un pezzo è difettoso, con quale probabilità esso proviene dallo stabilimento A?
  9. Il problema di Erone (matematico alessandrino vissuto probabilmente nella seconda metà del I secolo d.C.) consiste, assegnati nel piano due punti A e B, situati dalla stessa parte rispetto ad un retta r, nel determinare il cammino minimo che congiunge A con B toccando r. Si risolva il problema nel modo che si preferisce.
  10. Si provi che fra tutti i coni circolari retti circoscritti ad una sfera di raggio r, quello di minima area laterale ha il vertice che dista 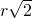r\sqrt 2 dalla superficie sferica.

 

 

 

Altri esercizi simili

 

(Questa pagina è stata visualizzata da 23 persone)

Lascia un commento