Quesito 10 P.N.I. 2012

0

Si provi che fra tutti i coni circolari retti circoscritti ad una sfera di raggio r, quello di minima area laterale ha il vertice che dista r\sqrt 2 dalla superficie sferica.

 

Sia CB=r raggio della circonferenza di base del cono

AB=a apotema

AK=x distanza del vertice dalla superficie della sfera.

Sappiamo che l’area laterale del cono è A_l=\pi R a.

Vogliamo quindi scrivere R e a in funzione di r, che è costante e x.

Osserviamo che:

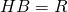  • HB=R per i criteri di congruenza.
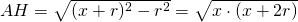  • AH=\sqrt {(x+r)^2-r^2}=\sqrt {x \cdot (x+2r)} per il teorema di Pitagora su AOH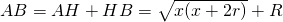
  • AB=AH+HB=\sqrt {x(x+2r)}+R

I triangoli ABC e AOH sono simili perchè rettangoli con un angolo in comune.

Sfruttiamo quindi la proporzione sui lati e otteniamo la relazione:

    \[CB:OH=AB:AO \Rightarrow $\frac R r = \frac {R+\sqrt {x(x+2r)}}{x+r}.\]

Da qui ricavo R in funzione di r e x:

    \[R\left (\frac 1r- \frac {1}{r+x}\right )=\frac {\sqrt {x(x+2r)}}{r+x} \Rightarrow R=\frac rx \sqrt {x(x+2r)}\]

    \[a=R+\sqrt {x(x+2r)}=\left(\frac rx+1 \right ) \sqrt {x(x+2r)}=\left( \frac {r+x}{r}\right)\sqrt {x}.\]

Allora:

    \[A_l=\pi Ra=\frac {r(r+x)(2r+x)\pi}{x}=\frac {r \pi}{x}(x^2+3rx+2r^2).\]

 

 

Altri esercizi simili

 

(Questa pagina è stata visualizzata da 23 persone)

Lascia un commento