La funzione ![]() è definita da
è definita da ![]() per tutti i numeri reali
per tutti i numeri reali ![]() appartenenti
appartenenti
all’intervallo chiuso [0, 9].
- Si tracci, in un sistema di coordinate cartesiane, il grafico Σ di
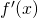 e da esso si deduca per quale o quali valori di
e da esso si deduca per quale o quali valori di  ,
, 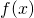 presenta massimi o minimi. Si tracci altresì l’andamento di
presenta massimi o minimi. Si tracci altresì l’andamento di 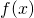 deducendolo da quello di
deducendolo da quello di 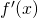 .
.
Considerando la funzione
![]()
,
ci accorgiamo subito che ci apprestiamo a costruire il grafico della funzione coseno con una dilatazione dovuta al coefficiente della x e una traslazione dovuta al termine noto.
GRAFICO
Per definizione sappiamo che i massimi per ![]() li otteniamo quando il segno della derivata diventa negativo e viceversa per i punti di minimo.
li otteniamo quando il segno della derivata diventa negativo e viceversa per i punti di minimo.
Quindi notiamo che, nel grafico appena disegnato, i punti di intersezione di questo stesso grafico con l’asse delle ascisse rappresentano proprio i valori per i quali avremo dei massimi o dei minimi nella funzione iniziale.
Studiamo quindi quando ![]() :
:
![]()
![]()
![]()
![]()
![]()
.
Essendo l’intervallo compreso tra 0 e 9, escludiamo subito tutte le soluzioni negative, e non possiamo prenderei in considerazione neanche soluzioni successive a queste perchè maggiori di 9.
Quindi, dal grafico di ![]() , si deduce che la funzione
, si deduce che la funzione ![]() in [0,9] ammette:
in [0,9] ammette:
- massimo in
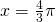
- minimo in
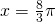 .
.
Si osservi che la funzione iniziale è facilmente calcolabile:
![]()
.
GRAFICO
Calcoliamo le coordinate del massimo e del minimo:
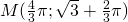
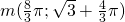 .
.
(Questa pagina è stata visualizzata da 23 persone)