Esame di maturità 2013: Problema 2 P.N.I. 2013

Sia $f$ la funzione definita per tutti gli $x$ positivi da $f (x) = x^3 ln x$ .

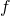Si studi $f$ e si tracci il suo grafico 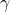$\gamma$ su un piano riferito ad un sistema di assi cartesiani ortogonali e monometrici 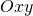$Oxy$ ; accertato che 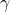$\gamma$ presenta sia un punto di flesso che un punto di minimo se ne calcolino, con l’aiuto di una calcolatrice, le ascisse arrotondate alla terza cifra decimale.
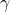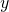Sia P il punto in cui $\gamma$ interseca l’asse $x$ . Si trovi l’equazione della parabola, con asse parallelo all’asse $y$ , passante per l’origine e tangente a 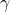$\gamma$ in P.
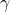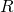Sia R la regione delimitata da $\gamma$ e dall’asse $x$ sull’intervallo aperto a sinistra ] 0, 1]. Si calcoli l’area di $R$ , illustrando il ragionamento seguito, e la si esprima in 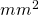$mm^2$ avendo supposto l’unità di misura lineare pari a 1 decimetro.
Si disegni la curva simmetrica di 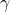$\gamma$ rispetto all’asse 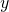$y$ e se ne scriva altresì l’equazione. Similmente si faccia per la curva simmetrica di 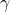$\gamma$ rispetto alla retta $y = -1$ .

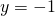Altri esercizi simili

(Questa pagina è stata visualizzata da 21 persone)

Matebook