Problema 2.4 P.N.I. 2013

Sia $f$ la funzione definita per tutti gli $x$ positivi da $f (x) = x^3 ln x$ .

Si disegni la curva simmetrica di $\gamma$ rispetto all’asse $y$ e se ne scriva altresì l’equazione. Similmente si faccia per la curva simmetrica di $\gamma$ rispetto alla retta $y = -1$ .

Chiamiamo $\gamma$ la prima curva richiesta (la simmetrica di f rispetto all’asse delle ordinate). Le equazioni di questa simmetria sono:

$\begin {cases}x'=-x \\ y'=y \end {cases}$

L’equazione di $\gamma$ è $g(x)=-x^3ln(-x)$ .

Chiamiamo $\gamma '$ la seconda curva richiesta (simmetrica di f rispetto alla retta $y=-1$ ). Le equazioni di questa simmetria sono:

$\begin {cases}x'=x \\ y'=-2-y \end {cases}$

L’equazione di $\gamma '$ è $h(x)=-2-x^3lnx$ .

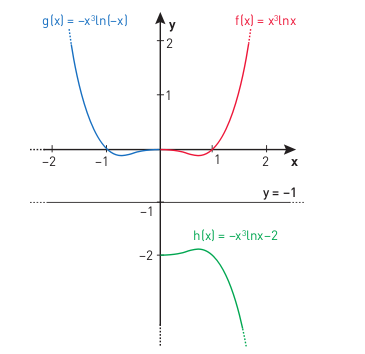
Di seguito i grafici.

Altri esercizi simili

(Questa pagina è stata visualizzata da 2 persone)

Matebook