Problema 2 Scientifico 2013

0

Sia f la funzione definita, per tutti gli x reali, da f(x )=\frac {8}{4+x^2}.

 

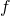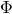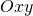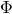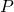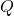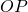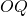  1. Si studi f e se ne disegni il grafico \Phi in un sistema di coordinate cartesiane Oxy . Si scrivano le equazioni delle tangenti a \Phi nei punti P (- 2; 1) e Q (2; 1) e si consideri il quadrilatero convesso che esse individuano con le rette OP e OQ . Si provi che tale quadrilatero è un rombo e si determinino le misure, in gradi e primi sessagesimali, dei suoi angoli.
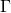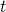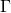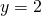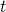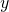  2. Sia \Gamma la circonferenza di raggio 1 e centro (0; 1). Una retta t , per l’origine degli assi, taglia \Gamma oltre che in O in un punto A e taglia la retta d’equazione y = 2 in un punto B. Si provi che, qualunque sia t , l’ascissa x di B e l’ordinata y di A sono le coordinate 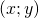(x; y) di un punto di \Phi.
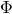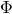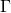  3. Si consideri la regione R compresa tra \Phi e l’asse x sull’intervallo [0, 2]. Si provi che R è equivalente al cerchio delimitato da \Gamma e si provi altresì che la regione compresa tra 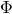\Phi e tutto l’asse x è equivalente a quattro volte il cerchio.
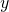  4. La regione R, ruotando attorno all’asse y , genera il solido 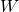W. Si scriva, spiegandone il perchè, ma senza calcolarlo, l’integrale definito che fornisce il volume di W.

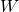Altri esercizi simili

(Questa pagina è stata visualizzata da 22 persone)

Lascia un commento