Si stabilisca per quali valori ![]() l’equazione
l’equazione ![]() ammette due soluzioni distinte
ammette due soluzioni distinte
appartenenti all’intervallo [0, 3]. Posto ![]() , si approssimi con due cifre decimali la maggiore
, si approssimi con due cifre decimali la maggiore
tali soluzioni, applicando uno dei metodi iterativi studiati.
Consideriamo la cubica:
![]()
.
Chiedere che l’equazione ![]() abbia due soluzioni distinte equivale a cercare per quali
abbia due soluzioni distinte equivale a cercare per quali ![]() la cubica
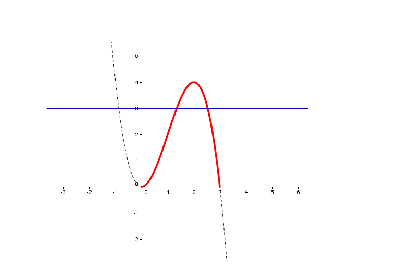
la cubica ![]() ha doppia intersezione con le rette orizzontali di livello k.
ha doppia intersezione con le rette orizzontali di livello k.
Dal disegno si osserva che k è compreso tra zero e il ![]() .
.
Determiniamo questo massimo.
![]()
Studiamo il segno della derivata:
![]()
![]()
da cui, avendo 2 soluzioni, 0 e 2, otteniamo:
dove il punto di massimo è ![]() .
.
![]()
Quindi avremo che:
![]() .
.
4 sarà da escludere altrimenti avrei due soluzioni coincidenti.
Sfruttando il metodo del punto medio in [2,3], dove si trova la maggiore delle soluzioni, ponendo ![]() avremo:
avremo:
![]()
![]() .
.
Per il teorema degli zeri, allora lo zero sarà un numero compreso tra 2 e 3.
Sia M il punto medio di [2;3], e quindi ![]() .
.
![]() .
.
Allora posso stimare lo zero di ![]() con
con ![]() che è il punto medio di
che è il punto medio di ![]() .
.
Altri esercizi simili
- Quesito 1 P.N.I. 2013
- Quesito 2 P.N.I. 2013
- Quesito 3 P.N.I. 2013
- Quesito 4 P.N.I. 2013
- Quesito 5 P.N.I. 2013
- Quesito 6 P.N.I. 2013
- Quesito 7 P.N.I. 2013
- Quesito 8 P.N.I. 2013
- Quesito 9 P.N.I. 2013
- Quesito 10 P.N.I. 2013
(Questa pagina è stata visualizzata da 7 persone)