Problema 2 P.N.I. 2014

0

Sia f(x)=(2-x) \sqrt{4x-x^2}

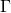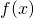  1. A lato è disegnato il grafico \Gamma di f(x). Si dimostri che 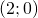(2; 0) è centro di simmetria di 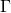\Gamma e si calcoli, in gradi e primi sessagesimali, l’angolo che la tangente in esso a 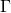\Gamma forma con la direzione positiva dell’asse x .
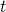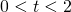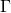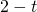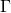  2. Si dimostri che, qualunque sia t, 0 < t< 2, le rette tangenti a \Gamma nei suoi punti di ascisse 2 -t e 2 +t sono parallele. Esistono rette tangenti a \Gamma che siano parallele alla retta  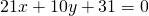21x +10y + 31 = 0? E che siano parallele alla retta 23x+12y + 35= 0?
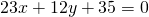  3. Si calcoli l’area della regione compresa tra \Gamma e l’asse x .
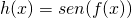  4. Sia h(x)= sen(f (x)). Quanti sono i punti del grafico di 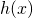h(x) di ordinata 1? Il grafico di 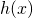h(x) presenta punti di minimo, assoluti o relativi? Per quali valori reali di k l’equazione 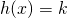h(x)= k ha 4 soluzioni distinte? Qual è il valore di \int_0^4 h(x) \, dx? 

     

     

     

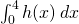    Altri esercizi simili

(Questa pagina è stata visualizzata da 1 persone)

Lascia un commento