Problema 2.1 Scientifico 2014

A lato è disegnato il grafico $\Gamma$ della funzione

$f(x)=x\sqrt{4-x^2}$

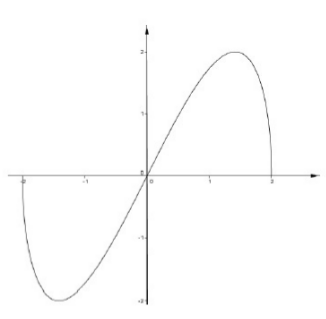
1. Si calcolino il massimo e il minimo assoluti di $f(x)$ .

Calcoliamo subito il dominio della funzione:

$4-x^2 \geq 0 \iff -2\leq x \leq 2$

il Dominio sarà quindi:

$[-2;2]$ .

Calcoliamo la derivata prima:

$f'(x)=\sqrt{4-x^2}+x\frac {-2x}{2\sqrt{4-x^2}}=\sqrt{4-x^2}-\frac {x^2}{\sqrt{4-x^2}}$

Vedendo il grafico, notiamo subito che i punti di massimo e minimo sono interni al dominio e quindi, risolvendo l’equazione $f'(x)=0$ , otteniamo:

$\frac{4-x^2-x^2}{\sqrt{4-x^2}}=0$

da cui:

$2x^2=4 \iff x=\pm \sqrt 2$

Essendo questi interni al dominio, allora questi saranno anche i massimi e minimi assoluti della funzione:

$max \, f=f(\sqrt2)=2$

$min \, f=f(-\sqrt2)=-2$

Altri esercizi simili

(Questa pagina è stata visualizzata da 4 persone)

Matebook