Problema 2.3 Scientifico 2014

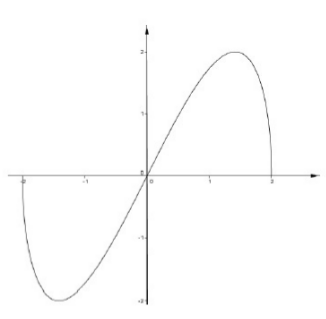
A lato è disegnato il grafico $\Gamma$ della funzione

$f(x)=x\sqrt{4-x^2}$

3. Si disegni la curva d’equazione $y^2=x^2(4-x^2)$ e si calcoli l’area della parte di piano da essa racchiusa.

Si nota subito come:

$y= \pm x\sqrt{4-x^2}$

e quindi, il grafico sarà dato dall’unione di $\Gamma$ e dal suo simmetrico rispetto all’asse delle x, formando una specie di 8.

Per il calcolo dell’area, vista la simmetria, le quattro parti in cui è divisa la figura dagli assi, sono equivalenti.

Studiamo solo la parte del primo quadrante:

$\int_0^2 x \sqrt{4-x^2}\, dx$

Sostituendo per comodità $x^2=t$ , da cui $2x\, dx= dt$ , otteniamo:

$\int_0^4 \frac 12(4-t)^{\frac 12} \, dt= \left[-\frac 12 \cdot \frac {(4-t)^{\frac 32}}{\frac 32}\right]_0^4=\frac 83.$

L’area totale sarà quindi $\frac {32}{3}$ .

Altri esercizi simili

(Questa pagina è stata visualizzata da 3 persone)

Matebook