Sia ![]() la funzione definita per tutti gli
la funzione definita per tutti gli ![]() positivi da
positivi da ![]() .
.
- Sia P il punto in cui
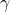 interseca l’asse
interseca l’asse  . Si trovi l’equazione della parabola, con asse parallelo all’asse
. Si trovi l’equazione della parabola, con asse parallelo all’asse 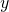 , passante per l’origine e tangente a
, passante per l’origine e tangente a 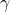 in P.
in P.
Si tratta di trovare ![]() dell’equazione generale della parabola
dell’equazione generale della parabola ![]() :
:
- impongo il passaggio per
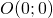 così da ottenere
così da ottenere 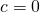
- impongo il passaggio per
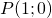 così da ottenere
così da ottenere 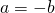
- impongo la tangenza in P alla parabola ottenuta
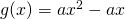 , ovvero impongo
, ovvero impongo 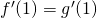 . Sostituendo ottengo
. Sostituendo ottengo 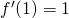 e poichè
e poichè 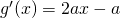 , otterrò
, otterrò 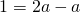 , da cui
, da cui 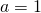 .
.
Dunque la parabola cercata è ![]() .
.
(Questa pagina è stata visualizzata da 1 persone)