Esercizi Nicola: esercizio con radicali

Pubblicato il da EdoLascia un commento
0

Svolgimento e soluzione di esercizi sui radicali

Corpo del messaggio:
Determina per quali valori di x \in R esistono le seguenti espressioni:

\sqrt{-x}+\sqrt[3]{\frac {1}{2x}}+\sqrt{-5-x}

\frac {1}{\sqrt {2x+1}}+\sqrt{x^2-4}

\frac {\sqrt{x^2-3x+2}}{\sqrt[3]{4-x}}

\sqrt {\frac {|x|}{9-x}}+\sqrt {-|x|+4}

 

Soluzione dallo staff

 

  • \sqrt{-x}+\sqrt[3]{\frac {1}{2x}}+\sqrt{-5-x}

Bisognerà studiare la positività dei radicandi con indice pari, mentre per quella con indice dispari basterà porre solo l’esistenza del denominatore.

\begin {cases} -x \geq 0 \\ 2x \neq 0 \\ -5-x \geq 0 \end {cases}

\begin {cases} x \leq 0 \\ x \neq 0 \\ -x \geq 5 \end {cases}

\begin {cases} x \leq 0 \\ x \neq 0 \\ x \leq -5 \end {cases}

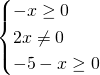
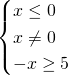
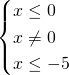
Intersecando le soluzioni, otterremo la soluzione richiesta:

x \leq -5.

 

  • \frac {1}{\sqrt {2x+1}}+\sqrt{x^2-4}

Bisognerà studiare la positività dei radicandi, con l’accortezza di guardare che, essendo una radice a denominatore, questa non può essere uguale a 0.

\begin {cases} 2x+1 > 0 \\ x^2-4 \geq 0 \end {cases}

\begin {cases} 2x > -1 \\ (x-2)(x+2) \geq 0 \end {cases}

\begin {cases} x > -\frac 12 \\ x \leq -2 \quad \lor \quad x \geq 2 \end {cases}

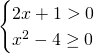
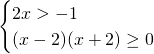
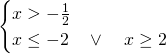
Intersecando le soluzioni, otterremo la soluzione richiesta:

x \geq 2.

 

  • \frac {\sqrt{x^2-3x+2}}{\sqrt[3]{4-x}}

Bisognerà studiare la positività del radicando con indice pari, mentre invece al denominatore basterà imporre che non può essere uguale a 0.

\begin {cases} x^2-3x+2 \geq 0 \\ 4-x \neq 0 \end {cases}

\begin {cases} (x-1)(x-2) \geq 0 \\ -x \neq -4 \end {cases}

\begin {cases} x \leq 1 \quad \lor \quad x \geq 2 \\ x \neq 4 \end {cases}

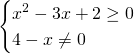
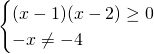
Intersecando le soluzioni, otterremo la soluzione richiesta:

x \leq 1 \quad \lor \quad x \geq 2 \mbox { con } x \neq 4.

 

  • \sqrt {\frac {|x|}{9-x}}+\sqrt {-|x|+4}

Nel primo radicando essendoci il valore assoluto al numeratore, basterà studiare solo la positività del denominatore, escludendo la possibilità che questo sia uguale a 0. Per il secondo radicando bisogna solo studiare la positività.

\begin {cases} \frac {|x|}{9-x} \geq 0 \\ -|x|+4 \geq 0 \end {cases}

\begin {cases} 9-x > 0 \\ -|x| \geq -4 \end {cases}

\begin {cases} -x > -9 \\ |x| \leq 4 \end {cases}

\begin {cases} x< 9 \\ -4 \leq x \leq 4 \end {cases}

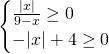
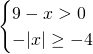
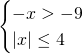
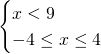
Intersecando le soluzioni, otterremo la soluzione richiesta:

-4 \leq x \leq 4.

 

(Questa pagina è stata visualizzata da 317 persone)

Lascia un commento