Federica scrive: Problema trapezio rettangolo

Uno studente scrive:

Oggetto: Problema

Corpo del messaggio:
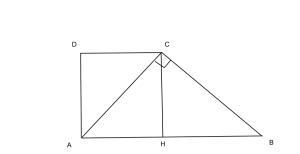
Disegna un trapezio rettangolo con la diagonale minore perpendicolare al lato obliquo. L’ altezza del trapezio è 3/4 della base minore e il lato obliquo è 3a. Calcola area e perimetro del trapezio.

Risposta dello staff

Dai dati avremo che, ponendo $DC=x$ :

$AD=CH=\frac 34 x$

$BC=3a$

$AH=x$

Possiamo subito calcolare la diagonale minore AC con il teorema di Pitagora:

$AC=\sqrt{AD^2+DC^2}=\sqrt{\frac {9}{16}x^2+x^2}=\sqrt{\frac {25}{16}x^2}=\frac 54 x$

Troviamo AB con il teorema di Euclide sul triangolo ABC:

$AB=\frac {AC^2}{AH}=\frac {\frac {25}{16}x^2}{x}=\frac {25}{16}x$

Ora che abbiamo tutto possiamo sfruttare il teorema di Pitagora su ABC per trovare l’incognita:

$AB^2=AC^2+BC^2$

$\frac {625}{256}x^2=\frac{25}{16}x^2+9a^2$

$\frac {625}{256}x^2-\frac{25}{16}x^2=9a^2$

$\frac {625-400}{256}x^2=9a^2$

$\frac {225}{256}x^2=9a^2$

Mettendo tutto sotto radice otteniamo:

$\frac {15}{16}x=3a$

$x=\frac {16}{5}a$

Quindi:

$AB=\frac {25}{16} x =5a$

$AD=\frac 34 x=\frac {12}{5}a$

Da cui:

$2p=5 a + 3a+\frac {16}{5}a+\frac {12}{5}a=\frac {68}{5}a$

$A=\frac {(5a+\frac {16}{5}a)\cdot \frac {12}{5}a}{2}=\frac {\frac {41}{5}a\cdot \frac {12}{5}a}{2}=\frac {246}{25}a^2$

(Questa pagina è stata visualizzata da 290 persone)

Matebook

La matematica spiegata passo passo

Federica scrive: Problema trapezio rettangolo

Risposta dello staff

Lascia un commento Annulla risposta