Uno studente scrive

Oggetto: Problemi con similitudini

Corpo del messaggio:
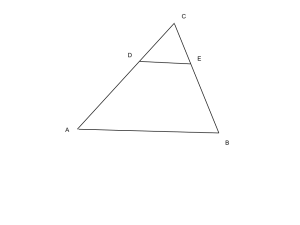
1)Dato il triangolo ABC di base AB e lato AC con AC=K, determina su AC un punto D tale che . Traccia dal punto D la parallela DE alla base. Calcola il rapporto fra le aree dei triangoli ABC e CDE.

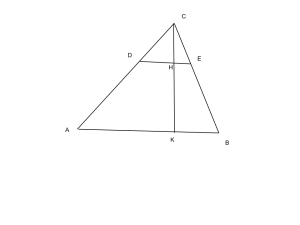
2)La base AB di un triangolo è lunga 10 cm. Una retta parallela alla base, che interseca i lati AC e BC nei punti D ed E, divide l’ altezza relativa alla base, CK, in due segmenti CH e HK il cui rapporto è . Determina la lunghezza della corda DE.

 

 

 

Risposta dello staff

1)  Sebbene questo problema possa risultare complicato per la mancanza di dati, a noi basterà trovare il rapporto tra 2 lati del triangolo e poi, elevando al quadrato, avremo il  rapporto delle due aree.

Quindi bisognerà trovare il rapporto tra AC e DC.

Sappiamo dai dati che

E quindi

Quindi, se il rapporto tra i lati sarà , mentre quello tra le aree sarà

.

 

 

 

 

Per definizione avremo che i triangoli CDE e ABC sono simili in quanto aventi un vertice uguale e costruiti con parallele di uno stesso lato.

Dai dati risulta che:

, e quindi:

Come abbiamo fatto per il problema precedente, riotteniamo tutto in funzione di un segmento del triangolo piccolo:

Quindi il rapporto tra 2 lati qualsiasi del triangolo è:

,

e lo stesso discorso verrà fatto anche per il segmento DE.

Quindi:

 

(Questa pagina è stata visualizzata da 456 persone)